
“Krumpli lelkem léptékinvariáns porhüvelye felett haranggörbe kondul.”
– Chuck Finley –

Ha kiválasztunk tetszés szerint ezer embert vagy lócitromot vagy ezer tányér rácpontyot tejföllel, és megmérjük egy-egy nemspecifikus fizikai jellemzőjüket (tömeg, térfogat, hossz, elektromos vezetőképesség, ízélmény stb.), akkor általában azt tapasztaljuk, hogy a legtöbb mért érték viszonylag közel esik egymáshoz. Lesz persze néhány közepesen eltérő, és elenyésző számú extrémen eltérő érték is, mindkét irányba, de a mérések nagy része az ún. számtani közép (magyarul: átlag) körüli értékhez esik majd közel. Minél nagyobb eltérést vizsgálunk az átlagtól, annál kevesebb elem hordozza majd azt a kirívó értéket. Köznapi és egyszerű példával élve: 1000 magyar férfit vizsgálva azt találnánk, hogy a magyar férfiak nagy része olyan 176 cm magas, vagy ennek az értéknek a közelében van a magassága. A 176 ± 10 cm sávba valószínűleg a vizsgált populáció 80%-a beletartozna. 165 cm-nél kisebb vagy 190 cm-nél magasabb egyének is lennének, de jóval kisebb számban, és még náluk is kevesebb lenne az olyan, aki mondjuk 210 cm-nél is magasabb vagy 150 cm-nél is kisebb. Ez, azt gondolom, mindenki által saját megfigyelései alapján elfogadható, szemléletes példa.
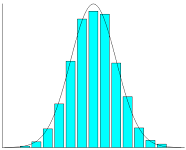
A mérési adatok ilyen típusú megoszlását normál eloszlásnak vagy más néven Gauss-eloszlásnak nevezik. (Gauss-papa intelmeiről és úgy általában: a tudománytörténet egyik, ha nem a legnagyobb zsenijéről is fogunk írni, csak mindenki győzze kivárni türelemmel.) Ha a mérési adatokat ábrázolnánk, egy jellegzetes alakzatot kapnánk, amit haranggörbének neveznek, lévén valóban görnyedtkígyó harang alakú a grafikon. Ilyenek a mérési grafikonok, a népesség fizikai paramétereit leíró adatsorok vagy épp az élőlények tűrésgrafikonjai. Régóta ismert és szeretett eloszlási mód ez, kidolgozott matematikai-statisztikai apparátussal. Valahányszor szórást, szórásnégyzetet, átlagot számolunk, t-próbát végzünk vagy megállapítjuk egy mérési adatsor relevanciáját, a Gauss által lefektetett alapokon elemezzük a normál eloszlású grafikonokat.
Nézzünk azonban egy másik jelenséget, s hívjuk segítségül a címbéli fagyott burgonyánkat. Képzeljük el, hogy egy jéggé fagyasztott krumplit földhöz csapunk. Akárha a nitrogénbe mártott higanyterminátor, számtalan kisebb-nagyobb darabra fog törni a termék. És most vizsgáljuk meg, milyen nagyságú darabok keletkeztek, milyen ezeknek az eloszlása. Egyáltalán nem normál eloszlást fogunk kapni, hanem valami egészen érdekes jellegzetességre figyelhetünk fel. Bármilyen méretet is választunk referenciaértéknek (legyenek mondjuk az 1 mm-es darabkák), azt tapasztalhatjuk, a méreteltéréssel valamilyen exponenciális függvény szerinti összefüggésben állnak a előforduló elemszámok. Ha ez marslakóul hangzik, akkor se rémüljünk meg: ez csak annyit tesz, hogy a kétszer akkora darabokból mondjuk negyedannyi van, a fele akkorákból négyszer annyi, a harmadakkorákból meg kilencszer annyi. Az igazán érdekes ebben az, hogy az exponenciális függvény ún. léptékinvariáns függvény, azaz BÁRHOL is válasszuk ki a referenciaméretet, ugyanezt fogjuk tapasztalni (Én egy időben ezt léptékirrelevánsnak neveztem, mert annak még értelme is volna, de sajnos ebbéli törekvésemet a tudományos világ csak igen szerény mértékben támogatja.)
Szemléletesebb, orvul lopott példával élve: ha mondjuk ember méretűek vagyunk és kimegyünk egy hegyre, látunk kisebb sziklákat, nagyobb sziklákat, kavicsokat, porszemeket. Meg tudjuk állapítani, hogy ezek méretei és darabszáma az említett exponenciális függvény szerint alakul, azaz a nálunk kétszer nagyobb sziklákból mondjuk nyolcadannyi van, mint a mi méretünkből, a fele akkorákból meg nyolcszor annyi. És most képzeljük el, hogy le tudjuk magunkat kicsinyíteni mondjuk a hupikék törpikék méretére. Körülnézve, ha nem számítjuk a növényzetet, azaz csak a sziklák alapján tájékozódnánk, nem is látnánk különbséget. Ugyanazt a méret-darabszám összefüggést figyelhetnénk meg, mint eddig. Ha a sok oda-vissza töpörítés-nagyítás közben elveszítenénk a fonalat, nem lenne lehetőség a mérések alapján, hogy megállapítsuk, melyik mérettartományban is vagyunk, hiszen az exponenciális függvény, mint azt írtam léptékinvariáns.
A DOW JONES index 3 havi és 1 éves trendje. Melyik nem lehetne a másik?
Talán még szemléletesebb példák a lázlapok vagy a tőzsdei index alakulásának grafikonjai. Bármely bróker megmondhatja, hogy ha figyeljük a tőzsdei papírok árfolyamának percenkénti alakulását, egy napra kivetítve egy lázgörbe-szerű szabálytalan grafikont kapunk, kisebb-nagyobb ingadozásokkal. És ha mellé rakunk egy éves grafikont, akkor ugyanezt az ábrát vagy nagyon hasonlót fogunk kapni, azaz nem lehet ránézésre eldönteni, milyen léptékben is vagyunk éppen. Az exponenciális rendszerek grafikai modellje a fraktál, ahol a legkisebb részletben is ott van az egész, és az egészben a legkisebb részlet. Hermész Triszmegisztosz szavaival: amiként lent, úgy fent is.
Az emberi lélek, már ha létezik, lett légyen isteni adomány avagy a neuronok bonyolult elektrokémiai folyamatai keltette öntudat, minden bizonnyal ilyen fagyott krumpli. Az emberi lélek léptékinvariáns: önnön maga mértéke és aránya.
Kapaszkodó nincs, reklamálni lehet Gaussnál.